📌 Research Themes: Do deep learning to have similar speech processing mechanisms as the human brain?
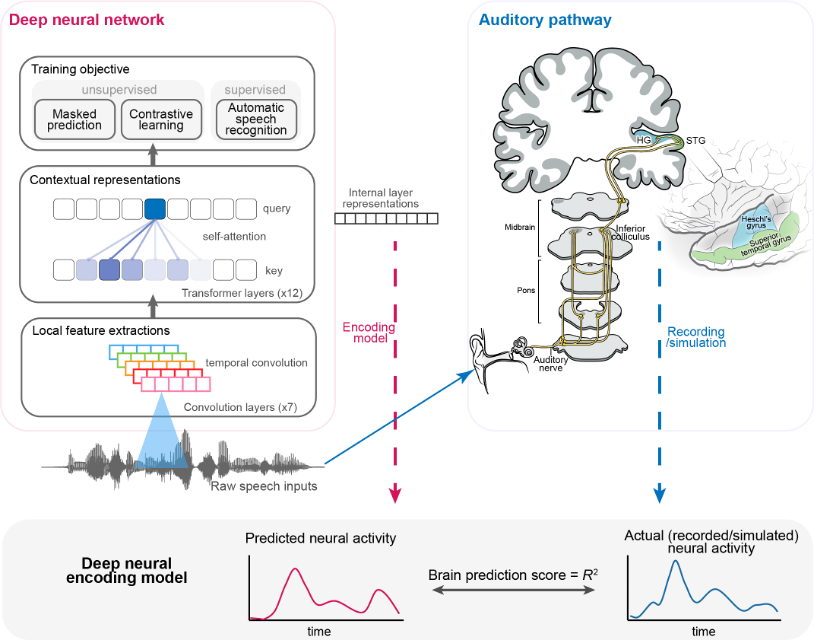
The neural activity in the human auditory pathway has a hierarchical structure. Different neural structures process and represent speech signals in a more complex and abstract manner as the hierarchy increases. Based on linguistic and phonological hypotheses or theories, neuroscientists extract features at different levels and analyze the encoding information in each stage of the pathway. Figure 1 illustrates several important processing areas of the human auditory pathway and their functions.
In the field of artificial intelligence, modern artificial intelligence (AI) models using deep neural networks (DNNs) and large amount of data are approaching human-level performance in automatic speech recognition. These data-driven models with their complex internal dynamic representations have caught the attention of neuroscientists. Many interesting research topics have been proposed, such as, Whether these AI models and the brain's auditory circuitry perform similar cognitive functions, is there computational and representational similarity between the two?
📌 A novel research methodology: Align deep learning representation with auditory neural activity.
This involves extracting feature representations from DNN pre-trained on speech, using these data-driven features to build new linear encoding models, and conducting correlation analysis with real brain auditory response signals. The aim is to explore the similarity between the intrinsic feature representations and the neural population activity in different brain auditory pathways, offering new data-driven computational models of sensory perception.
To gain a deeper understanding of this research method, this page implements two research projects. The first one uses behavioral data to quantitatively compare automated speech recognition models, and the second one uses ECoG recordings to align the hierarchical representations of DNN and the human auditory pathway. In the local implementation process, you need to download some datasets and code repositories, and a GPU may also be required. Based on the original papers, I also added some recent works, such as the OpenAI Whisper model.
Mainly based on the following two publications, which have very friendly data and code access methods. I modified the code and added explanations. Please note that due to limitations in data access, the full extent of the original research may not be represented here. Therefore, if you find that certain information from papers has been omitted, please understand that I am doing my best to interpret the content. Overall, this page will focus on the implementation of specific research topics to better showcase this research methodology. I believe within this framework, there will be many interesting research topics in the future.
Juliette Millet and Ewan Dunbar. Do self-supervised speech models develop human-like perception biases? AAAI 2022 Workshop, Self-Supervised Learning for Audio and Speech Processing, 2022.
Li, Y., Anumanchipalli, G., Mohamed, A., Chen, P., Carney, L. H., Lu, J., Wu, J., Chang, E.F. (2023) Dissecting neural computations of the human auditory pathway using deep neural networks for speech. Nature Neuroscience, 26, 1-30.
Part One: Do self-supervised speech models develop human-like perception biases?¶
1.Introduction¶
Under the influence of their native languages, human listeners develop biases in speech perception. For instance:
- Japanese native speakers have a tendency to confuse the English sounds /r/ and /l/ (Yamada and Tohkura, 1990). Therefore, words like "right" and "light" in English may be perceived as the same or very similar by Japanese speakers.
- On the other hand, English native speakers struggle with the French contrast between /y/ and /u/ (Levy, 2009). They have difficulty perceiving the distinction between words like "rue" (/y/: meaning "street") and "roue" (/u/: meaning "wheel").
These perceptual biases emerge early in the process of acquiring the native language: infants older than six months exhibit a facilitation effect in discriminating sounds of their native language, but show a decline in discriminating certain non-native sounds (Kuhl et al., 2006). Because these improvements in native language sounds and declines in non-native language sounds appear to have positive implications for infants' future language abilities (Tsao et al., 2004; Kuhl et al., 2005), having a perceptual space biased towards the native language may be crucial for accurately perceiving and understanding native language speech in various situations, including environmental noise and speaker variability.
Self-supervised models are currently the most advanced speech processing models, which construct a representation space from a large amount of unlabeled data and demonstrate near-human-level performance on tasks such as speech recognition. Representations obtained through self-supervised pre-training possess human-like flexibility and adaptability. Models fine-tuned on English data can further enhance performance on English, but at the cost of reduced discrimination ability for other potential languages. While it is easy to explain this observation from the perspective of data distribution, we are more interested in the relationship between this observation and the perceptual biases developed by humans.
Exploring whether self-supervised models have similar biases as humans in their native language is very interesting.
The question to address is: Does the language data used for training affect self-supervised speech models in a similar way as it does for human listeners' native language?
2.Method¶
I will abstract the experimental method into the following process, with specific details becoming clearer as progress is made.
- Speech stimuli experiments to obtain participants' behavioral data.
- Self-supervised model stimuli experiments to simulate human discrimination behavior towards phonemes.
- Comparison of these two performances.
3.Preparation¶
Clone the github repo and download dataset according to the README.
git clone https://github.com/JAMJU/Sel_supervised_models_perception_biases.git
4.Human ABX test¶
The probes of human speech perception involves ABX phoneme discrimination tests, in which participants listen to three speech segments: A, B, and X (an A/B/X triplet). A and B always differ by only one phoneme, while X always has the same phoneme sequence as either A or B (e.g., A: /pap/, B: /pip/, X: /pap/). Participants are asked to identify which of the first two sounds (A or B) is most similar to the last sound (X). The pair of stimuli, p1:p2, is referred to as a contrast.
The stimulus data is obtained from the Perceptimatic Dataset, which contains behavioral data from phoneme discrimination tasks in six different languages. In total, there are 662 phoneme contrasts and the corresponding stimulus sounds used in the experiments. The focus of this paper is on monolingual participants who are native speakers of French and English.
import tqdm
import os
import torch
import numpy as np
#
filename_triplet_list = "triplet_data.csv" # opensource
dataset_path = "dataset"
get_func = None
distance = None
def read_csv(filename):
lines = open(filename, 'r').readlines()
ind = lines[0].strip().split(',')
data = []
for line in lines[1:]:
data.append({name:value for name, value in zip(ind, line.strip().split(',')) })
return data
lines = read_csv(filename_triplet_list)
print(f"Number of Triplet Data:{len(lines)}")
print("Triplet Data Sample:")
for name, value in lines[0].items():
print(f"\t{name}:\t\t{value}")
Number of Triplet Data:8461 Triplet Data Sample: : 0 triplet_id: triplet_83_B TGT_item: amelia_consonants_10.wav OTH_item: amelia_consonants_28.wav X_item: ewan_58.wav speaker_TGT: amelia speaker_OTH: amelia speaker_X: ewan language_TGT: EN language_OTH: EN language_X: EN TGT_first: False dataset: pilot-aug-2018
we can see that the data includes 8461 triplets.
According to the paper, the dataset consists of 4231 distinct triplets. This is half of 8461 because each triplet is sometimes presented to participants in the order of target/other/X and sometimes in the order of other/target/X.
TGT_item refers to the audio file A containing the target phoneme sequence, OTH_item refers to the audio file B used for confusion, and X_item is the one with the same phoneme sequence as file A. Additionally, the data includes speaker and language information. Let's listen to them and try to experience it.
from IPython.display import Audio, display
sample_data = lines[0]
TGT_func = lambda x : os.path.join(dataset_path, x["dataset"], "wavs_extracted", x["TGT_item"])
OTH_func = lambda x : os.path.join(dataset_path, x["dataset"], "wavs_extracted", x["OTH_item"])
X_func = lambda x : os.path.join(dataset_path, x["dataset"], "wavs_extracted", x["X_item"])
TGT_audio_sample = TGT_func(sample_data)
OTH_audio_sample = OTH_func(sample_data)
X_audio_sample = X_func(sample_data)
print("Sample A:")
display(Audio(filename=TGT_audio_sample,rate=16000))
print("Sample B:")
display(Audio(filename=OTH_audio_sample,rate=16000))
print("Sample X:")
display(Audio(filename=X_audio_sample,rate=16000))
Sample A:
Sample B:
Sample X:
It sounds like A and X are the same, /atɑ/. The one in the middle sounds like /afɑ/.
Now let's take a look at the experimental results corresponding to these stimuli.
human_and_models_filename = "humans_and_models/file_data.csv" # opensource
human_and_models_data = read_csv(human_and_models_filename)
print(f"Number of Human Behavioural Experiments:{len(human_and_models_data)}")
for i in human_and_models_data:
if 'triplet_83_B' == i["triplet_id"]:
print("Data Sample (triplet_83_B):")
for name, value in i.items():
print(f"\t{name}:\t\t\t\t{value}")
break
Number of Human Behavioural Experiments:87631 Data Sample (triplet_83_B): : 0 subject_id: X_IHTYDKWOUB subject_language: EN triplet_id: triplet_83_B TGT_item: amelia_consonants_10.wav OTH_item: amelia_consonants_28.wav X_item: ewan_58.wav speaker_TGT: amelia speaker_OTH: amelia speaker_X: ewan language_TGT: EN language_OTH: EN language_X: EN TGT_first: False user_ans: 1 bin_user_ans: 1 phone_TGT: t phone_OTH: f phone_X: t prev_phone: a next_phone: ɑ context: a_ɑ nb_stimuli: 0 dataset: pilot-aug-2018 deepspeech_englishtxt_rnn4: 0.15936934043274648 wav2vec_english_transf4: 0.12251163941376364 deepspeech_frenchtxt_rnn4: 0.1629706981896903 cpc_french_AR: 0.05872012213169375 wav2vec_french_transf4: 0.04093575305274538 hubert_french_transf_5: 0.04855605986577621 cpc_audioset_AR: -0.020788736911799943 mfccs_la: -0.0025078723330559174 cpc_english_AR: 0.050190139536198775 hubert_english_transf_5: 0.08956584890180974 wav2vec_audioset_transf4: 0.0319468904371876 hubert_audioset_transf_5: 0.04221348163325256 deepspeech_french_rnn4: 0.18394535542149 deepspeech_english_rnn4: 0.18102908468174178
These stimuli generated 87631 behavioral trials. We also examined the first behavioral experiment results of the previous Triplet stimuli. Compared to before, we obtained more information:
prev_phoneandnext_phonedetermine what we just heard.prev_phoneandnext_phoneform the context.user_ansis 1, indicating that the listener chose the first option.
In addition, this test included 662 phoneme comparisons, 259 French participants, and 280 English participants. Note that there are also many long floating-point numbers displayed above, but you can ignore them for now.
5.Perceptualizing Speech with Self-Supervised Models¶
Now we begin to let the self-supervised model perceive these stimuli. Here is a convenient method to use these powerful speech models, taking wav2vec2 as an example. As you can see, importing the model only takes two lines of code. This model is pretrained and fine-tuned on 960 hours of Librispeech with 16kHz sampled speech audio, it can be considered representative of English native speakers.
from transformers import Wav2Vec2Processor, Wav2Vec2ForCTC
import soundfile as sf
# load model and tokenizer
processor = Wav2Vec2Processor.from_pretrained("facebook/wav2vec2-base-960h")
model = Wav2Vec2ForCTC.from_pretrained("facebook/wav2vec2-base-960h").eval()
# read target audio with soundfiles
TGT_audio_data, sr = sf.read(TGT_audio_sample)
# tokenize
input_values = processor(TGT_audio_data, return_tensors="pt", padding="longest").input_values # Batch size 1
# retrieve model output including logits and hidden representation
output = model(input_values, output_hidden_states=True)
Ignored unknown kwarg option normalize Ignored unknown kwarg option normalize Ignored unknown kwarg option normalize Ignored unknown kwarg option normalize
Some weights of Wav2Vec2ForCTC were not initialized from the model checkpoint at facebook/wav2vec2-base-960h and are newly initialized: ['wav2vec2.masked_spec_embed'] You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference. It is strongly recommended to pass the ``sampling_rate`` argument to this function. Failing to do so can result in silent errors that might be hard to debug.
The model perceives the TGT_audio_sample, which is the /ata/ we just heard. Let's see how wav2vec2 interpreted it.
logits = output.logits
# take argmax and decode
predicted_ids = torch.argmax(logits, dim=-1)
transcription = processor.batch_decode(predicted_ids)
print(f"transcription:{transcription}")
transcription:['AHTA']
it interpreted it as /AHTA/, which looks quite good and close to what we heard. Generally, when studying the representation of deep neural networks, we usually explore a specific layer within the model. wav2vec2 is a model that only has an encoder, and its layers can be viewed using the following command:
print(model.wav2vec2.encoder.layers)
# hidden state
print(f"# of Layers:{len(output.hidden_states)}")
print(f"Shape of each Layer:{output.hidden_states[0].shape}")
ModuleList(
(0-11): 12 x Wav2Vec2EncoderLayer(
(attention): Wav2Vec2Attention(
(k_proj): Linear(in_features=768, out_features=768, bias=True)
(v_proj): Linear(in_features=768, out_features=768, bias=True)
(q_proj): Linear(in_features=768, out_features=768, bias=True)
(out_proj): Linear(in_features=768, out_features=768, bias=True)
)
(dropout): Dropout(p=0.1, inplace=False)
(layer_norm): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
(feed_forward): Wav2Vec2FeedForward(
(intermediate_dropout): Dropout(p=0.1, inplace=False)
(intermediate_dense): Linear(in_features=768, out_features=3072, bias=True)
(intermediate_act_fn): GELUActivation()
(output_dense): Linear(in_features=3072, out_features=768, bias=True)
(output_dropout): Dropout(p=0.1, inplace=False)
)
(final_layer_norm): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
)
)
# of Layers:13
Shape of each Layer:torch.Size([1, 31, 768])
wav2vec2 has a stacked 12 layers of Wav2Vec2EncoderLayer, but here the output of the fifth layer is chosen for this experiment.
For the TGT_audio_sample, the self-supervised model wav2vec2 obtains a representation feature with 31 time steps and 768 dimensions at each time point. To quickly get more perceptual results, we package these operations into a function. Meanwhile, functions related to common used MFCC features are also shown below.
def get_wav2vec_representation(audio_sample, layer=-1):
audio_data, sr = sf.read(audio_sample)
input_values = processor(audio_data, sampling_rate=16000, return_tensors="pt", padding="longest").input_values # Batch size 1
output = model(input_values, output_hidden_states=True)
return output.hidden_states[layer].squeeze().detach()
import librosa
def get_mfcc_representation(filename,layer=-1):
y, sr = librosa.load(filename)
spect = librosa.feature.mfcc(
y=y,
sr=16000,
n_mfcc=13,
win_length=int(0.025 * sr),
hop_length=int(0.010 * sr),
)
spect = spect.T
return spect
TGT = get_wav2vec_representation(TGT_audio_sample, layer=6)
OTH = get_wav2vec_representation(OTH_audio_sample, layer=6)
X = get_wav2vec_representation(X_audio_sample, layer=6)
TGT.shape, OTH.shape, X.shape
(torch.Size([31, 768]), torch.Size([34, 768]), torch.Size([25, 768]))
Recalling the experimental approach to human perception of speech:+
Given an A/B/X triplet, participants are asked to identify which of the two options, A or B, is more similar to X.
This is straightforward for humans, but machines cannot directly tell us which one is similar to X. Given an ABX triplet, we now have three representations
- A:[31, 768]
- B:[34, 768]
- C:[25, 768]
and an objective measure based on these representations needs to be designed. It should reflect the property of "which one is similar to X". Clearly, using metrics like "mean squared error" directly is not feasible because they have different time scales. One approach to address this issue is Dynamic Time Warping(DTW).

Image from: Rakthanmanon et al. “Searching and Mining Trillions of Time Series Subsequences under Dynamic Time Warping”, Figure 3.
For the sake of clarity, let's consider A/B/C as one-dimensional features. We can think of representation A as Q, which is the red waveform, and representation C as C, which is the blue line. Because the speech content of AC is the same, both being /ata/, they should be very similar. However, they may have a different number of data points (31 vs 25) due to temporal offset. Even if they had the same number of data points, we would still get a large distance, similar to what is shown in the top left. In other words, the results of direct calculation will return as they have a "significant difference."
DTW can align them well, as shown in the bottom left, connecting corresponding time points. Now, the distance obtained at these points is a mroe resonable measure of the difference between them. The right graph shows the temporal correspondence. So it is easy to understand the following formula:
$$ \Delta = \mathrm{DTW}(M_{other}, M_X) - \mathrm{DTW}(M_{target}, M_X)$$
Here DTW aggregate frame-level cosine distances along the warping path to obtain the distance. The larger the $\Delta$ value (more positive), the better the model's ability to distinguish between the target and other phoneme categories.
from dtw_experiment import compute_dtw
TGT = get_wav2vec_representation(TGT_audio_sample, layer=6)
OTH = get_wav2vec_representation(OTH_audio_sample, layer=6)
X = get_wav2vec_representation(X_audio_sample, layer=6)
distance = "cosine"
TGTX = compute_dtw(TGT, X, distance, norm_div=True)
OTHX = compute_dtw(OTH, X, distance, norm_div=True)
wav2vec_delta = OTHX - TGTX
wav2vec_delta
0.07953007742150814
By using the above formula, we obtained the results of the self-supervised model's perception of speech. wav2vec2 considers A to be similar to X at the confident level of $\Delta$. Do you remember those numbers we saw in the experimental results corresponding to the stimuli? Yes, those are the results of the speech model.
hubert_english_transf_5: 0.08956584890180974
cpc_french_AR: 0.05872012213169375
From this particular case, it seems that the ability to discriminate phoneme contrast of wav2vec2 lies between these two models (this is an informal statement).
from dtw_experiment import compute_dtw
TGT = get_mfcc_representation(TGT_audio_sample)
OTH = get_mfcc_representation(OTH_audio_sample)
X = get_mfcc_representation(X_audio_sample)
distance = "cosine"
TGTX = compute_dtw(TGT, X, distance, norm_div=True)
OTHX = compute_dtw(OTH, X, distance, norm_div=True)
mfcc_delta = OTHX - TGTX
mfcc_delta
-0.0028166435984554386
Moreover, the performance of the MFCC is almost consistent with the publicly available results. This demonstrates the reliability of these codes.
Furthermore, Open AI Whisper, which is currently one of the strongest speech recognition models, has also been taken into consideration
from transformers import WhisperProcessor, WhisperForConditionalGeneration
import soundfile as sf
processor = WhisperProcessor.from_pretrained("openai/whisper-large-v2")
model = WhisperForConditionalGeneration.from_pretrained("openai/whisper-large-v2")
model.config.forced_decoder_ids = None
sample = TGT_audio_sample
audio_data, sr = sf.read(sample)
input_features = processor(audio_data, sampling_rate=16000, return_tensors="pt").input_features
# generate token ids
predicted_ids = model.generate(inputs=input_features, output_hidden_states=True)
# decode token ids to text
transcription = processor.batch_decode(predicted_ids, skip_special_tokens=False)
['<|startoftranscript|><|en|><|transcribe|><|notimestamps|> .<|endoftext|>']
transcription = processor.batch_decode(predicted_ids, skip_special_tokens=True)
transcription
[' ATA']
def get_whiser_representation(audio_sample, layer=-1):
audio_data, sr = sf.read(audio_sample)
input_features_nopad = processor(audio_data, sampling_rate=16000, padding="do_not_pad", return_tensors="pt").input_features
input_features = processor(audio_data, sampling_rate=16000, return_tensors="pt").input_features
decoder_input_ids = torch.tensor([[1, 1]]) * model.config.decoder_start_token_id
output = model(input_features, output_hidden_states=True, decoder_input_ids=decoder_input_ids)
return output.encoder_last_hidden_state[:,:input_features_nopad[0].shape[1],:].squeeze().detach()
from dtw_experiment import compute_dtw
TGT = get_whiser_representation(TGT_audio_sample)
OTH = get_whiser_representation(OTH_audio_sample)
X = get_whiser_representation(X_audio_sample)
distance = "cosine"
TGTX = compute_dtw(TGT, X, distance, norm_div=True)
OTHX = compute_dtw(OTH, X, distance, norm_div=True)
whisper_delta = OTHX - TGTX
whisper_delta
-0.018564086530874824
The performance does not seem to be that impressive. Due to the extensive computational requirement of over 24 hours, I have temporarily put aside this part of the work. Exploring the speech perception mechanism of Whisper would be very interesting, as it does not belong to the self-supervised model category. Its superior performance suggests that it may have developed unique processing methods or perhaps it develops an inspired perceptual patterns as self-supervised method.
Let's go back to the earlier part. Now that we know how to make the speech model perceive each speech stimulus, computing the results on the entire dataset is just a loop code.
from dtw_experiment import compute_dtw
def get_delta(
TGT_audio_sample,
OTH_audio_sample,
X_audio_sample,
func):
TGT = func(TGT_audio_sample)
OTH = func(OTH_audio_sample)
X = func(X_audio_sample)
distance = "cosine"
TGTX = compute_dtw(TGT, X, distance, norm_div=True)
OTHX = compute_dtw(OTH, X, distance, norm_div=True)
delta = OTHX - TGTX
return delta
triplets_data = read_csv(filename_triplet_list)
triplets_result = {}
func = get_mfcc_representation
for triplet_item in tqdm.tqdm(triplets_data, desc="Computing delta values...."):
TGT_audio_sample = TGT_func(triplet_item)
OTH_audio_sample = OTH_func(triplet_item)
X_audio_sample = X_func(triplet_item)
triplets_result[triplet_item["triplet_id"]] = get_delta(TGT_audio_sample,OTH_audio_sample,X_audio_sample,func)
for item in human_and_models_data:
#item[model_name] = triplets_result[item["triplet_id"]]
for k in item:
if k in ["TGT_first", "subject_id", "dataset"]: continue
try:
item[k] = float(item[k])
except:
pass
6.Comparing humans and models’ perceptual¶
Two metrics are used to evaluate the extent to which the representation space of the self-supervised model matches the perceptual space of humans in speech. (See Paper Sec. 5.2)。
- the log-likelihood
- the Spearman correlation (ρ)
6.1.The log-likelihood¶
For the self-supervised model, we computed a metric $\Delta$. If $\Delta$ can accurately predict the choice outcomes of human behavioral experiments, it indicates that the self-supervised model can effectively predict human performance. That is, the similarity between the model's representation space and the participants' perceptual space is significant.
Since the participants' responses are discrete (correct or incorrect), probit regression is used to fit the participants' binary responses.
- Question: Why not use the commonly used linear regression?
We attempted to directly use linear regression for processing. Let the dependent variable be the correctness or incorrectness of the listener's answer, and
$$ \begin{equation} y = \left\{ \begin{array}{**lr**} 1 & \mathrm{Correct} \\ 0 & \mathrm{Incorrect} \end{array} \right. \nonumber \end{equation} $$
The factors influencing $y$ are denoted as $x=(x_1,x_2,...,x_n)$ (individual samples are not marked here for simplicity), resulting in the equation of a multiple regression (Linear Probability Model).
$$ \begin{equation} y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + + \beta_n x_n + \epsilon \nonumber \end{equation} $$
Where $(\beta_1,\beta_2,...,\beta_n)^T=\boldsymbol \beta$ represents the regression parameters, $\epsilon$ represents the error term. Using the vector form, we have
$$ \begin{equation} y = \beta_0 + \boldsymbol \beta \mathbf x + \epsilon \nonumber \end{equation} $$
According to the assumption of zero mean for the random error term:$\mathbb{E}(\epsilon|\mathbf x)=0$, we have
$$ \begin{equation} \mathbb{E}(y|\mathbf x) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n \nonumber \end{equation} $$
Let $\hat(y)_i$ denote the predicted value, and the corresponding loss function is given by
$$ \begin{equation} Q = \sum^n_1(y_i - \hat{y}_i)^2 = \sum^n_1(y_i - (\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n))^2 \nonumber \end{equation} $$
Estimate a set of parameters that minimizes the loss function, and denote them as $(\hat{\beta_0},\hat{\beta_1},\hat{\beta_2},...,\hat{\beta_n})$
Since the value of $y$ is either 0 or 1, let the probability value corresponding to $y=1$ be $p$, so the probability value corresponding to $y=0$ is $1-p$. Therefore, we have
$$ \begin{align} \mathbb{E}(y) & = 0 \times (1-p) + 1 \times p \\ & = p \\ & = P(y=1|\mathbf x) \\ & = \hat{y} \\ & = \hat{\beta_0} + \hat{\beta_1} x_1 + \hat{\beta_2} x_2 + ... + + \hat{\beta_n} x_n \nonumber \end{align} $$
It appears that, holding other factors constant, $\beta_i$ represents the impact of the change in $x_i$ on the probability $P(y=1)$ of the participant's answer being correct:
$$ \begin{equation} \Delta P(y=1|\mathbf x) = \beta_i \Delta x_i \nonumber \end{equation} $$
In this model, $\beta_i$ represents the expected change in $y$ when $x_i$ increases by one unit, without considering the influence of other variables. This effect is constant and independent with the change of $x$.
However, this assumption is unrealistic because $y$ is a discrete variable with values in the range of $[0,1]$, not in the real domain. If the values of $x$ are very large or very small, the linear probability model may predict values of $y$ that exceed the range of $[0,1]$, which is not meaningful. This implies that directly using a regular linear regression model for modeling binary dependent variables is problematic (and includes other issues as well).
2.Question: What is binary Probit regression?
Since LPM cannot guarantee that the predicted values of $y$ fall within the range of $[0,1]$, we can use a transformation function $\Phi$ to project them. A classic choice is the standard normal distribution.
$$P(y=1|\mathbf x) = \Phi (\mathbf x \beta) = \int_{-\inf}^{\mathbf x \beta} \frac{1}{\sqrt{2\pi}} \mathrm{exp}(-\frac{z^2}{2})dz\tag {1}$$
This is the Probit model. To estimate the parameters $\beta$, we can use the maximum likelihood method and construct the likelihood function as follows:
$$ L (\beta)=\prod_ {i=1}^ {n}P (y_i=1|\mathrm x_ {i})^ {y_i} [1-P (y_i=1|\mathrm x_ {i})]^ {1-y_i}\tag {2}$$
Substituting equation (1) into equation (2), we have:
$$L (\beta)=\prod_ {i=1}^ {n}[\Phi (\mathrm x_ {i}\beta)]^ {y_i} [1-\Phi (\mathrm x_ {i}\beta)]^ {1-y_i}\tag {3}$$
For convenience, we can take the logarithm of the likelihood function to obtain the log-likelihood function:
$$ \ln L (\beta)=\sum_ {i=1}^ {n}[y_i\ln \Phi (\mathrm x_ {i} \beta)+(1-y_i)\ln (1-\Phi (\mathrm x_ {i}\beta))]\tag {4}$$
Our goal is to find the $\beta$ values that maximize the log-likelihood function, known as the maximum likelihood estimation. Since the log-likelihood function does not have an analytical solution, we can only solve it using numerical methods such as Newton's method or quasi-Newton methods.
After obtaining the parameters, the Log-Likelihood on the sample set represents the model's ability to predict experimental data. In other words, the larger the Log-Likelihood, the more the model parameters can explain the data variation.
The $\Delta$ value, calculated based on the model representation, is used as a predictor variable. In addition to the global intercept, the regression also utilizes other predictor variables to explain:
- Whether the correct answer is A (1) or B (0);
- The order of the experiment in the experimental list;
- A categorical predictor variable for the participants;
- An annotation of which Perceptimatic subset it belongs to.
During the usage, it is necessary to map some variables to the range of [0,1] and standardize them. The log-likelihood is obtained from the fitted regression model. The larger the log-likelihood (the smaller the negative value), the better the $\Delta$ value predicts the experimental data given the model. In other words, the model can better predict human performance. Therefore, the model's representation space is more similar to the perceptual space of the experimental participants. Furthermore, it can be used to compare different models and see which model can better fit the data.
from multiprocessing import Pool
import pandas as pd
from statsmodels.formula.api import probit
from sampling import get_dico_corres_file, sample_lines
model_name = "wav2vec_audioset_transf4"
dico_lines = get_dico_corres_file(human_and_models_filename, french=False, english = True)
lines_sampled = sample_lines(dico_lines)
data_ = pd.DataFrame(human_and_models_data)
data_['bin_user_ans'] = (data_['bin_user_ans'] + 1.) / 2 # we transform -1 1 into 0 1
data_['TGT_first'] = data_['TGT_first'].astype(bool)
data_['TGT_first_code'] = data_['TGT_first'].astype(int)
data = data_.iloc[lines_sampled]
data_worker = data.copy()
# normalize data
for val in ['nb_stimuli', model_name]:
data_worker[val] = (data[val] -data[val].mean())/data[val].std()
The statsmodels library in Python provides a convenient probit API. The code utilizes the $\Delta$ values of wav2vec_audioset_transf4 and the three features mentioned above as predictor variables.
# we create the probit model
model_probit = probit("bin_user_ans ~ C(subject_id) + C(dataset) + nb_stimuli + " + model_name, data_worker)
result_probit = model_probit.fit_regularized(max_iter=200, disp=True)
loglikehood = model_probit.loglike(result_probit.params)
Optimization terminated successfully (Exit mode 0)
Current function value: 0.5095092161564122
Iterations: 644
Function evaluations: 644
Gradient evaluations: 644
result_probit.summary()
| Dep. Variable: | bin_user_ans | No. Observations: | 42305 |
|---|---|---|---|
| Model: | Probit | Df Residuals: | 42019 |
| Method: | MLE | Df Model: | 285 |
| Date: | Tue, 07 Nov 2023 | Pseudo R-squ.: | 0.06204 |
| Time: | 11:10:08 | Log-Likelihood: | -21555. |
| converged: | True | LL-Null: | -22981. |
| Covariance Type: | nonrobust | LLR p-value: | 0.000 |
In the results, we can see that the value of Log-Likelihood is -21623. This value does not have a straightforward interpretation, but we can compare the performance with other models and refer to the results presented in the paper. Here, we can directly load the pre-computed results.
# pre calculated result
result_filename = "results.csv"
with open(result_filename, "r") as f:
lines = f.readlines()
idxs = lines[0].strip().split(",")[1:]
result_data = []
for line in lines[1:]: result_data.append([float(_) for _ in line.strip().split(",")][1:])
mean = np.average(result_data, axis=0)
variance = np.var(result_data, axis=0)
x = np.arange(len(idxs))
rank_data = [[i,j] for i,j in zip(mean, idxs)]
rank_data = sorted(rank_data, key=lambda x : -x[0])
mean, idxs = [round(_[0]) for _ in rank_data], [_[1] for _ in rank_data]
from pyecharts.globals import CurrentConfig, NotebookType
CurrentConfig.NOTEBOOK_TYPE = NotebookType.JUPYTER_LAB
from pyecharts.charts import Bar
from pyecharts import options as opts
bar = (
Bar(init_opts=opts.InitOpts())
.add_xaxis(idxs)
.add_yaxis("Log-likelihood values (shorter bars are better)", mean)
.set_global_opts(title_opts=opts.TitleOpts(
title="Log-likelihood values", subtitle="For English participants"),
xaxis_opts=opts.AxisOpts(axislabel_opts=opts.LabelOpts(rotate=-90)),
yaxis_opts=opts.AxisOpts(min_=-21700, max_=-20000)
)
)
bar.load_javascript()
bar.render("bar_chart_1.html")
'/ssd9/exec/penglinkai/brain_sci/Sel_supervised_models_perception_biases/bar_chart_1.html'
from IPython.display import IFrame
IFrame(src='./bar_chart_1.html', width=1000, height=600)
It can be observed that for English participants, the model trained on English data has a better fit. This result supports the statement that self-supervised models trained on English data exhibit English language biases similar to humans.
6.2.The Spearman correlation (ρ)¶
This section calculates the Spearman's correlation coefficient (Spearman's ρ) between the model's $\Delta$ values and participant accuracy. The calculation is performed at the level of each phone contrast. Specifically,
import pandas as pd
from scipy.stats import spearmanr
data = pd.read_csv(human_and_models_filename)
dico_lines_french = get_dico_corres_file(human_and_models_filename, french=True, english=False)
dico_lines_english = get_dico_corres_file(human_and_models_filename, french=False, english=True)
list_sampled_english = sample_lines(dico_lines_english)
dff = data.iloc[list_sampled_english]
value_evaluated = "wav2vec_audioset_transf4"
# We get only what we need
dff = dff[[
'triplet_id',
'phone_TGT',
'phone_OTH',
'prev_phone',
'next_phone',
'language_OTH',
'language_TGT',
'dataset',
'user_ans',
value_evaluated]]
# We adapt to some dataset that have a -3 / 3 scale
dff.loc[dff['dataset'] == "WorldVowels", ['user_ans']] = dff.loc[dff['dataset'] == "WorldVowels", ['user_ans']] / 3.
dff.loc[dff['dataset'] == "zerospeech", ['user_ans']] = dff.loc[dff['dataset'] == "zerospeech", ['user_ans']] / 3.
This part of the code selects triplet_id,phone_TGT,phone_OTH,prev_phone,next_phone,language_OTH,language_TGT,dataset,user_ans as the grouping criteria.
# We average over triplet first
gf = dff.groupby([
'triplet_id',
'phone_TGT',
'phone_OTH',
'prev_phone',
'next_phone',
'language_OTH',
'language_TGT',
'dataset'], as_index = False)
ans_fr = gf.user_ans.mean()
val_fr = gf[value_evaluated].mean()
ans_fr[value_evaluated] = val_fr[value_evaluated]
len(list(gf)),list(gf)[0]
(8461,
(('BR_TRIP10222_0', 'e', 'ĩ', 's', 'k', 'BR', 'BR', 'WorldVowels'),
triplet_id phone_TGT phone_OTH prev_phone next_phone language_OTH \
26129 BR_TRIP10222_0 e ĩ s k BR
29265 BR_TRIP10222_0 e ĩ s k BR
29265 BR_TRIP10222_0 e ĩ s k BR
26129 BR_TRIP10222_0 e ĩ s k BR
28658 BR_TRIP10222_0 e ĩ s k BR
language_TGT dataset user_ans wav2vec_audioset_transf4
26129 BR WorldVowels -0.333333 0.031396
29265 BR WorldVowels 0.666667 0.031396
29265 BR WorldVowels 0.666667 0.031396
26129 BR WorldVowels -0.333333 0.031396
28658 BR WorldVowels 1.000000 0.031396 ))
The expression len(list(gf)) represents the number of distinct groups in the grouping results, which is 8461 in total. list(gf)[0] shows several experimental results belonging to the first group. The data is averaged over user_ans and value_evaluated (wav2vec_audioset_transf4). The results are displayed below.
ans_fr
| triplet_id | phone_TGT | phone_OTH | prev_phone | next_phone | language_OTH | language_TGT | dataset | user_ans | wav2vec_audioset_transf4 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | BR_TRIP10222_0 | e | ĩ | s | k | BR | BR | WorldVowels | 3.333333e-01 | 0.031396 |
| 1 | BR_TRIP10222_1 | e | ĩ | s | k | BR | BR | WorldVowels | 2.000000e-01 | 0.031396 |
| 2 | BR_TRIP10726_0 | i | ɛ | d | s | BR | BR | WorldVowels | 9.333333e-01 | 0.054557 |
| 3 | BR_TRIP10726_1 | i | ɛ | d | s | BR | BR | WorldVowels | 9.333333e-01 | 0.054557 |
| 4 | BR_TRIP10775_0 | i | e | d | s | BR | BR | WorldVowels | -6.666667e-02 | 0.019795 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 8456 | triplet_FR995 | y | l | t | e | FR | FR | zerospeech | 4.440892e-17 | 0.034653 |
| 8457 | triplet_FR996 | y | l | t | e | FR | FR | zerospeech | 4.440892e-17 | 0.034653 |
| 8458 | triplet_FR997 | y | l | p | d | FR | FR | zerospeech | -6.666667e-02 | -0.024223 |
| 8459 | triplet_FR998 | y | l | p | d | FR | FR | zerospeech | 2.666667e-01 | -0.024223 |
| 8460 | triplet_FR999 | y | l | s | i | FR | FR | zerospeech | 7.333333e-01 | 0.027158 |
8461 rows × 10 columns
In this step, triplet_id is merged, and phone_TGT,phone_OTH,prev_phone,next_phone,language_OTH,language_TGT,dataset are used as the grouping criteria.
# Then we average over context
gf = ans_fr.groupby([
'phone_TGT',
'phone_OTH',
'prev_phone',
'next_phone',
'language_OTH',
'language_TGT',
'dataset'], as_index = False)
ans_fr = gf.user_ans.mean()
val_fr = gf[value_evaluated].mean()
ans_fr[value_evaluated] = val_fr[value_evaluated]
len(list(gf)),list(gf)[0]
(3401,
(('a', 'aː', 'f', 'f', 'GL', 'GL', 'WorldVowels'),
triplet_id phone_TGT phone_OTH prev_phone next_phone language_OTH \
1998 GL_TRIP1548_0 a aː f f GL
1999 GL_TRIP1548_1 a aː f f GL
2026 GL_TRIP2165_0 a aː f f GL
2027 GL_TRIP2165_1 a aː f f GL
2114 GL_TRIP945_0 a aː f f GL
2115 GL_TRIP945_1 a aː f f GL
language_TGT dataset user_ans wav2vec_audioset_transf4
1998 GL WorldVowels 0.866667 -0.005935
1999 GL WorldVowels 0.733333 -0.005935
2026 GL WorldVowels 0.266667 0.062786
2027 GL WorldVowels 0.133333 0.062786
2114 GL WorldVowels 0.533333 0.020428
2115 GL WorldVowels 0.600000 0.020428 ))
The expression len(list(gf)) represents the number of distinct groups in the grouping results, which is 3401 in total. list(gf)[0] shows several experimental results belonging to the first group. The data is averaged again over user_ans and value_evaluated (wav2vec_audioset_transf4). The results are displayed below.
ans_fr
| phone_TGT | phone_OTH | prev_phone | next_phone | language_OTH | language_TGT | dataset | user_ans | wav2vec_audioset_transf4 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | a | aː | f | f | GL | GL | WorldVowels | 0.522222 | 0.025759 |
| 1 | a | aː | g | g | GL | GL | WorldVowels | 0.322222 | 0.044892 |
| 2 | a | aː | p | p | GL | GL | WorldVowels | 0.200000 | -0.005515 |
| 3 | a | e | d | k | FR | FR | zerospeech | -0.066667 | 0.011050 |
| 4 | a | e | i | d | FR | FR | zerospeech | 0.500000 | 0.054048 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 3396 | θ | s | a | ɑ | EN | EN | pilot-aug-2018 | -0.600000 | 0.009272 |
| 3397 | θ | s | i | i | EN | EN | pilot-aug-2018 | 1.000000 | 0.017195 |
| 3398 | θ | t | i | i | EN | EN | pilot-aug-2018 | 0.400000 | 0.055567 |
| 3399 | θ | ʃ | a | ɑ | EN | EN | pilot-aug-2018 | 1.000000 | 0.010789 |
| 3400 | θ | ʃ | i | i | EN | EN | pilot-aug-2018 | 0.200000 | 0.011312 |
3401 rows × 9 columns
Here, prev_phone and next_phone are merged to focus on phone contrasts.
# then we average over phone contrast
gf = ans_fr.groupby([
'phone_TGT',
'phone_OTH',
'language_OTH',
'language_TGT',
'dataset'], as_index=False)
ans_fr = gf.user_ans.mean()
val_fr = gf[value_evaluated].mean()
ans_fr[value_evaluated] = val_fr[value_evaluated]
len(list(gf)),list(gf)[0]
(1285,
(('a', 'aː', 'GL', 'GL', 'WorldVowels'),
phone_TGT phone_OTH prev_phone next_phone language_OTH language_TGT \
0 a aː f f GL GL
1 a aː g g GL GL
2 a aː p p GL GL
dataset user_ans wav2vec_audioset_transf4
0 WorldVowels 0.522222 0.025759
1 WorldVowels 0.322222 0.044892
2 WorldVowels 0.200000 -0.005515 ))
ans_fr
| phone_TGT | phone_OTH | language_OTH | language_TGT | dataset | user_ans | wav2vec_audioset_transf4 | |
|---|---|---|---|---|---|---|---|
| 0 | a | aː | GL | GL | WorldVowels | 0.348148 | 0.021712 |
| 1 | a | e | FR | FR | zerospeech | 0.311111 | 0.036211 |
| 2 | a | i | EN_DR2 | EN_DR2 | pilot-july-2018 | 0.466667 | 0.033544 |
| 3 | a | i | EN_DR3 | EN_DR3 | pilot-july-2018 | 0.200000 | 0.073582 |
| 4 | a | i | EN_DR7 | EN_DR7 | pilot-july-2018 | 0.200000 | 0.090170 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 1280 | θ | k | EN | EN | pilot-aug-2018 | 0.600000 | 0.003462 |
| 1281 | θ | p | EN | EN | pilot-aug-2018 | 0.600000 | 0.023903 |
| 1282 | θ | s | EN | EN | pilot-aug-2018 | 0.200000 | 0.013234 |
| 1283 | θ | t | EN | EN | pilot-aug-2018 | 0.400000 | 0.055567 |
| 1284 | θ | ʃ | EN | EN | pilot-aug-2018 | 0.600000 | 0.011051 |
1285 rows × 7 columns
# the we average over order TGT-OTH or the other way around
res = ans_fr.copy()
res['phone_TGT'] = ans_fr['phone_OTH']
res['phone_OTH'] = ans_fr['phone_TGT']
res['language_OTH'] = ans_fr['language_TGT']
res['language_TGT'] = ans_fr['language_OTH']
total = pd.concat([ans_fr, res], axis=0)
gf = total.groupby(['phone_TGT', 'phone_OTH', 'language_OTH','language_TGT', 'dataset'], as_index=False)
ans_fr = gf.user_ans.mean()
val_fr = gf[value_evaluated].mean()
ans_fr[value_evaluated] = val_fr[value_evaluated]
ans_fr
| phone_TGT | phone_OTH | language_OTH | language_TGT | dataset | user_ans | wav2vec_audioset_transf4 | |
|---|---|---|---|---|---|---|---|
| 0 | a | aː | GL | GL | WorldVowels | 0.201852 | 0.003995 |
| 1 | a | e | FR | FR | zerospeech | 0.438889 | 0.009876 |
| 2 | a | i | EN_DR2 | EN_DR2 | pilot-july-2018 | 0.633333 | 0.053046 |
| 3 | a | i | EN_DR3 | EN_DR3 | pilot-july-2018 | 0.200000 | 0.073582 |
| 4 | a | i | EN_DR4 | EN_DR4 | pilot-july-2018 | 0.600000 | 0.068183 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 1319 | θ | k | EN | EN | pilot-aug-2018 | 0.700000 | 0.010990 |
| 1320 | θ | p | EN | EN | pilot-aug-2018 | 0.600000 | 0.018190 |
| 1321 | θ | s | EN | EN | pilot-aug-2018 | 0.600000 | 0.022778 |
| 1322 | θ | t | EN | EN | pilot-aug-2018 | 0.500000 | 0.038148 |
| 1323 | θ | ʃ | EN | EN | pilot-aug-2018 | 0.600000 | 0.038617 |
1324 rows × 7 columns
Finally, by ignoring the order of TGT-OTH, we obtained experimental results for 1324 phone contrasts pairs. The Spearman's correlation coefficient (spearmanr) is then calculated between the model's $\Delta$ values and participant responses.
rho_fr, p_fr = spearmanr(ans_fr['user_ans'], ans_fr[value_evaluated])
print(value_evaluated, rho_fr, p_fr)
wav2vec_audioset_transf4 0.3842111077640824 8.016630361775731e-48
"0.227" seems to be a not very significant result. Let's put the results of other models together and see the performance.
# pre calculated result
result_filename = "beginning_outfile_english.csv"
with open(result_filename, "r") as f:
lines = f.readlines()
idxs = lines[0].strip().split(",")[1:]
result_data = []
for line in lines[1:]: result_data.append([float(_) for _ in line.strip().split(",")][1:])
mean = [round(_, 3) for _ in np.average(result_data, axis=0)]
variance = np.var(result_data, axis=0)
x = np.arange(len(idxs))
rank_data = [[i,j] for i,j in zip(mean, idxs)]
rank_data = sorted(rank_data, key=lambda x : -x[0])
mean, idxs = [_[0] for _ in rank_data], [_[1] for _ in rank_data]
from pyecharts.globals import CurrentConfig, NotebookType
CurrentConfig.NOTEBOOK_TYPE = NotebookType.JUPYTER_LAB
from pyecharts.charts import Bar
from pyecharts import options as opts
bar = (
Bar(init_opts=opts.InitOpts())
.add_xaxis(idxs)
.add_yaxis("the Spearman correlation (ρ)", mean)
.set_global_opts(title_opts=opts.TitleOpts(
title="the Spearman correlation (ρ)"),
xaxis_opts=opts.AxisOpts(axislabel_opts=opts.LabelOpts(rotate=-90)),
yaxis_opts=opts.AxisOpts(min_=0.3, max_=0.6)
)
)
bar.load_javascript()
bar.render("bar_chart_2.html")
'/ssd9/exec/penglinkai/brain_sci/Sel_supervised_models_perception_biases/bar_chart_2.html'
from IPython.display import IFrame
IFrame(src='./bar_chart_2.html', width=1000, height=600)
In this section, for each model, we calculate the Pearson correlation coefficient between its native language effect and the native language effect of human listeners. The closer the correlation coefficient is to 1, the better the given model captures phone-level native language effects. Here, the performance of the self-supervised model is worse compared to the generic MFCC features. This suggests that at the level of phone contrast, the self-supervised model fails to capture some component of human speech perception.
7.Native language effect¶
In the above section, we conducted a global evaluation to measure the alignment between the model's representation space and the perceptual space of human listeners. In this section, we assess whether the model can replicate the native language preferences exhibited by human participants.
Specifically, we evaluate models trained on French and English data separately to determine if they exhibit the same biased behavior as French and English native speakers. The general approach is as follows:
- The $\Delta$ values for each model will be normalized for comparison between models.
- For each phone contrast pair, the overall accuracy is calculated.
- For each phone contrast pair, the average $\Delta$ value of the French-trained model is subtracted from the average $\Delta$ value of the English model. The same operation is performed for the accuracy of English participants and French participants. This value can be considered as the native language effect on a specific phone contrast pair.
- For each model, the Pearson correlation coefficient is computed between the native language effect of each phone contrast pair and that of human listeners.
The closer the correlation coefficient is to 1, the better the given model captures phonemic-level native language effects.
data = pd.read_csv(human_and_models_filename, sep=',', encoding='utf-8')
dico_lines_french = get_dico_corres_file(human_and_models_filename, french=True, english=False)
dico_lines_english = get_dico_corres_file(human_and_models_filename, french=False, english=True)
list_sampled_french = sample_lines(dico_lines_french)
list_sampled_english = sample_lines(dico_lines_english)
lines_sampled = list_sampled_french + list_sampled_english
data = data.iloc[lines_sampled]
data.loc[data['dataset'] == "WorldVowels", ['user_ans']] = data.loc[data['dataset'] == "WorldVowels", ['user_ans']] / 3.
data.loc[data['dataset'] == "zerospeech", ['user_ans']] = data.loc[data['dataset'] == "zerospeech", ['user_ans']] / 3.
data_fr = data[data['subject_language'] == 'FR'].copy()
data_en = data[data['subject_language'] == 'EN'].copy()
dico_models = {'wav2vec_transf4':{'english':'wav2vec_english_transf4', 'french':'wav2vec_french_transf4'},
'hubert':{'english':'hubert_english_transf_5', 'french':'hubert_french_transf_5'},
'deepspeech_phon':{'english':'deepspeech_english_rnn4', 'french':'deepspeech_french_rnn4'},
'cpc':{'english':'cpc_english_AR', 'french':'cpc_french_AR'},
'deepspeech_txt': {'english': 'deepspeech_englishtxt_rnn4', 'french': 'deepspeech_frenchtxt_rnn4'},
}
values_comparison_english = [dico_models[modi]['english'] for modi in dico_models]
values_comparison_french = [dico_models[modi]['french'] for modi in dico_models]
# We normalize english and french side for the model so they are comparable
for i in range(len(values_comparison_english)):
data_fr[values_comparison_french[i]] = data_fr[values_comparison_french[i]] / data_fr[
values_comparison_french[i]].std()
data_en[values_comparison_english[i]] = data_en[values_comparison_english[i]] / data_en[
values_comparison_english[i]].std()
# Select data interested, same as above cells
data_en['contrast'] = data_en['phone_TGT'] + ';' + data_en['phone_OTH'] + ';' + data_en['language_OTH'] + ';' + data_en['language_TGT'] + ';' + data_en[ 'dataset']
data_fr['contrast'] = data_fr['phone_TGT'] + ';' + data_fr['phone_OTH'] + ';' + data_fr['language_OTH'] + ';' + data_fr['language_TGT'] + ';' + data_fr[ 'dataset']
# construct contrast data
data_fr_contrast = {}
data_en_contrast = {}
# assign a empty dict for later uses
for k in values_comparison_french + ['user_ans']:
data_fr_contrast[k] = {}
for k in values_comparison_english + ['user_ans']:
data_en_contrast[k] = {}
# loop each item, aggregate each contrast for each model
for idx in range(len(data_en)):
item = data_en.iloc[idx]
contrast = item['contrast'].replace('"', "")
for k in values_comparison_english + ['user_ans']:
delta = float(item[k])
data_en_contrast[k][contrast] = data_en_contrast[k].get(contrast, []) + [delta] # same as append()
for idx in range(len(data_fr)):
item = data_fr.iloc[idx]
contrast = item['contrast'].replace('"', "")
for k in values_comparison_french + ['user_ans']:
delta = float(item[k])
data_fr_contrast[k][contrast] = data_fr_contrast[k].get(contrast, []) + [delta] # same as append()
# sample
# {'wav2vec_english_transf4': {
# 'i;ʊ;EN_DR7;EN_DR7;pilot-july-2018': [0.7581879995638313,0.7581879995638313,0.7581879995638313],
# 'ʊ;ʌ;EN_DR7;EN_DR7;pilot-july-2018': [0.44245396646602203,0.32058457305888916,0.32058457305888916],
# 'a;u;EN_DR2;EN_DR2;pilot-july-2018': [0.3934868173149888,0.3934868173149888,0.3934868173149888],
# 'æ;ʊ;EN_DR5;EN_DR5;pilot-july-2018': [0.7740108224569093,0.7740108224569093,0.7740108224569093],
# ...
# we average the results
for k in values_comparison_english + ['user_ans']:
for cont in data_en_contrast[k]:
data_en_contrast[k][cont] = np.asarray(data_en_contrast[k][cont]).mean()
for k in values_comparison_french + ['user_ans']:
for cont in data_fr_contrast[k]:
data_fr_contrast[k][cont] = np.asarray(data_fr_contrast[k][cont]).mean()
# sample
# {'wav2vec_english_transf4': {
# 'i;ʊ;EN_DR7;EN_DR7;pilot-july-2018': 1.3776102894272364,
# 'ʊ;ʌ;EN_DR7;EN_DR7;pilot-july-2018': 0.44245396646602203,
# 'a;u;EN_DR2;EN_DR2;pilot-july-2018': 2.9639408282294744,
# 'æ;ʊ;EN_DR5;EN_DR5;pilot-july-2018': 0.7740108224569093,
The averages $\Delta$ for each phone contrast pair have been computed, and the values related to native language effects are calculated below.
triplet_list = list(data_en_contrast[values_comparison_english[0]].keys())
diff_humans = []
diff_models = {}
for i in range(len(values_comparison_english)):
diff_models[values_comparison_english[i]] = []
triplet_done = []
diffs = []
for trip in triplet_list:
if trip in triplet_done:
continue
# we average on TGT-OTH OTH-TGT
other = trip.split(';')
other = ';'.join([other[1], other[0], other[3], other[2], other[4]])
triplet_done.append(other)
triplet_done.append(trip)
if trip in data_fr_contrast['user_ans'] and not trip in data_en_contrast['user_ans']:
print('ERROR triplet not test on eng', trip)
continue
elif trip not in data_fr_contrast['user_ans'] and trip in data_en_contrast[
'user_ans']:
print('ERROR triplet not test on fre', trip)
continue
elif trip not in data_fr_contrast['user_ans'] and trip not in data_en_contrast[
'user_ans']:
print('ERROR triplet not test on fre and on en', trip)
continue
val_fr_human = (data_fr_contrast['user_ans'][trip] + data_fr_contrast['user_ans'].get(other, data_fr_contrast['user_ans'][trip])) / 2.
val_en_human = (data_en_contrast['user_ans'][trip] + data_en_contrast['user_ans'].get(other,data_en_contrast['user_ans'][trip])) / 2.
diff_humans.append(val_fr_human - val_en_human)
for i in range(len(values_comparison_english)):
# average on TGT-OTH OTH-TGT
val_fr_model = (data_fr_contrast[values_comparison_french[i]][trip] +
data_fr_contrast[values_comparison_french[i]].get(other,data_fr_contrast[values_comparison_french[i]][trip])) / 2.
val_en_model = (data_en_contrast[values_comparison_english[i]][trip] +
data_en_contrast[values_comparison_english[i]].get(other,data_en_contrast[values_comparison_english[i]][trip])) / 2.
# core code
diff_models[values_comparison_english[i]].append(val_fr_model - val_en_model)
diffs += [np.asarray(diff_humans)]
for i in range(len(values_comparison_english)):
diffs += [diff_models[values_comparison_english[i]]]
The Pearson correlation coefficient is calculated between the native language effect of each phone contrast pair and that of human listeners.“
from scipy.stats import pearsonr
rs = []
diff_humans = diffs[0]
for i in range(len((dico_models.keys()))):
r, p = pearsonr(diffs[i+1], diff_humans)
rs.append(r)
print(r,p)
0.015723982716882613 0.6863389024697809 0.040789548947215024 0.29466542980729943 0.09660902151954646 0.01288942527914428 0.07633362519653619 0.049626580245979955 0.09889294029729122 0.010900056633808195
# pre calculated result
result_filename = "file_out.csv"
with open(result_filename, "r") as f:
lines = f.readlines()
idxs = lines[0].strip().split(",")[1:]
result_data = []
for line in lines[1:]: result_data.append([float(_) for _ in line.strip().split(",")][1:])
mean = np.mean(result_data, axis=0)
mean = [mean[_] for _ in [0,2,4,6,8]]
idxs = [idxs[_] for _ in [0,2,4,6,8]]
from pyecharts.globals import CurrentConfig, NotebookType
CurrentConfig.NOTEBOOK_TYPE = NotebookType.JUPYTER_LAB
from pyecharts.charts import Bar
from pyecharts import options as opts
bar = (
Bar(init_opts=opts.InitOpts())
.add_xaxis(idxs)
.add_yaxis("Native language effect", mean)
.set_global_opts(title_opts=opts.TitleOpts(
title="Native language effect"),
xaxis_opts=opts.AxisOpts(axislabel_opts=opts.LabelOpts(rotate=-90)),
yaxis_opts=opts.AxisOpts(min_=0.0, max_=0.6)
)
)
bar.load_javascript()
bar.render("bar_chart_4.html")
'/ssd9/exec/penglinkai/brain_sci/Sel_supervised_models_perception_biases/bar_chart_4.html'
from IPython.display import IFrame
IFrame(src='./bar_chart_4.html', width=1000, height=600)
The figure above shows the evaluation of native language effects on the entire Perceptimatic dataset (see Figure 4 in the paper). CPC and DeepSpeech exhibit similar abilities to discriminate between groups. However, Hubert and Wav2Vec2 do not show significant native language effects. This result is consistent with expectations, as large-scale unsupervised speech models already possess strong, language-agnostic discriminative abilities during pre-training. Compared to 60,000 hours of pre-training data, 600 hours of supervised training may have little impact on the earlier transformer layers.
8.Conclusion¶
Based on the experimental results, the following findings were observed:
Self-supervised models trained on speech recordings perform better in discriminating speech sounds and predicting human discrimination behavior compared to models trained on non-speech sounds (soundscapes).
At the stimulus level, self-supervised models perform well in predicting human discrimination behavior, but they perform worse than neutral acoustic features in terms of average human results for each phone contrast.
Self-supervised models show little influence from training languages (native languages). In other words, their prediction ability is not affected by the training language.
These results suggest that self-supervised speech models are able to mimic human listener's perceptual preferences to some extent, but there are still gaps in certain aspects. Particularly, self-supervised models are relatively weaker in predicting the overall trends of human discrimination behavior. The training language of self-supervised models has little impact on their prediction ability, indicating a certain universality of their understanding of speech features across different languages.
Part Two: Dissecting neural computations of the human auditory pathway using deep neural networks for speech¶
Part One of the study examined the similarity between the representation space of DNNs and human perception from the perspective of speech stimulus and human behavior experiments. In this part, we will be dealing with electroencephalogram (EEG) signals and analyzing the relationship between hierarchical representations in DNN layers and the auditory pathway in the human auditory system.
1.Speech Stimuli¶
see Section: Experimental paradigm
In the experiment, participants were instructed to passively listen to continuous speech stimuli. No other tasks were performed during the passive listening process. The acoustic stimuli used in the study consisted of natural continuous American English and Mandarin Chinese. The English speech stimuli were derived from the TIMIT dataset, which includes 499 English sentences selected from the TIMIT corpus and read by 402 different speakers (286 males and 116 females). There was a 0.4-second silence between sentences. The task was divided into five blocks, each lasting approximately 5 minutes.
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
%matplotlib inline
from scipy.stats import zscore, ttest_rel, f_oneway, ttest_ind
from scipy.signal import resample
from scipy.io import wavfile
from asccd import timit, preanalysis, erps, plotting, util
from asccd import temporal_receptive_field as trf
timit_annotation = timit.get_timit_annotations()
timit_annotation
| time | pitch | intensity | log_hz | erb_rate | rel_pitch_global | rel_pitch_global_erb | abs_pitch | abs_pitch_erb | abs_pitch_change | ... | front | low | back | plosive | fricative | syllabic | nasal | voiced | obstruent | sonorant | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fadg0_si1279 | 0 | 0.01 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0.02 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0.03 | NaN | 32.27 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0.04 | NaN | 32.68 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 0.05 | NaN | 30.99 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| mzmb0_si1796 | 186 | 1.87 | NaN | 33.69 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 187 | 1.88 | NaN | 32.45 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 188 | 1.89 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 189 | 1.90 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 190 | 1.91 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
101961 rows × 27 columns
timit_annotation.keys()
Index(['time', 'pitch', 'intensity', 'log_hz', 'erb_rate', 'rel_pitch_global',
'rel_pitch_global_erb', 'abs_pitch', 'abs_pitch_erb',
'abs_pitch_change', 'abs_pitch_erb_change', 'zscore_intensity', 'phn',
'dorsal', 'coronal', 'labial', 'high', 'front', 'low', 'back',
'plosive', 'fricative', 'syllabic', 'nasal', 'voiced', 'obstruent',
'sonorant'],
dtype='object')
The data was pre-labeled. In addition to acoustic parameters such as pitch, intensity, log_hz, erb_rate, rel_pitch_global, rel_pitch_global_erb, abs_pitch, abs_pitch_erb, abs_pitch_change, abs_pitch_erb_change, and zscore_intensity, articulation features were labeled using a 0/1 encoding scheme. Articulation features is a group of property of a speech sound based on its voicing or on its place or manner of articulation in the vocal tract, as voiceless, bilabial, or stop used in describing the sound. A practical application scenario is that: When processing non-native speaker speech production data, they can be used to diagnose pronunciation errors in second language learners.
Each row represents a time frame of 0.01 seconds, and the beginning contains the sentence information labeled in the TIMIT dataset. We can calculate the number of sentences used and the duration of the speech stimuli.
num_sentences = len(set([i[0] for i in timit_annotation.to_dict()["time"].keys()]))
print("# of Timit dataset used:", num_sentences)
print("Play Druation of Timit dataset used:", len(timit_annotation)/100 + (num_sentences - 1) * 0.04)
# of Timit dataset used: 499 Play Druation of Timit dataset used: 1039.53
"499" This number corresponds to the report in the literature.
based on the level of time frames, we aim to obtain information at the phoneme and syllable levels. This provides the foundation for subsequent hierarchical representation analysis.
timit_syllables = timit.load_timit_syllables()
timit_syllables
| start_times | end_times | syllable_phns | ||
|---|---|---|---|---|
| timit_name | syllable_index | |||
| mmds0_si1973 | 0 | 0.132250 | 0.230187 | dh ax-h q |
| 1 | 0.230187 | 0.260813 | eh | |
| 2 | 0.260813 | 0.318500 | nx ih | |
| 3 | 0.318500 | 0.458813 | m iy | |
| 4 | 0.458813 | 0.672687 | dcl d ih dcl | |
| ... | ... | ... | ... | ... |
| mbma1_si2207 | 0 | 0.143063 | 0.337375 | ae z |
| 1 | 0.337375 | 0.484500 | w iy | |
| 2 | 0.484500 | 0.720000 | ey tcl | |
| 3 | 0.720000 | 0.827000 | w iy | |
| 4 | 0.827000 | 1.317937 | tcl t ao kcl t |
4233 rows × 3 columns
timit_phonemes = timit.get_timit_phonemes()
timit_phonemes
| start_time | end_time | phn | silence | ||
|---|---|---|---|---|---|
| timit_name | phoneme_index | ||||
| makr0_si1352 | 0 | 0.000000 | 0.150000 | h# | True |
| 1 | 0.150000 | 0.250625 | ae | False | |
| 2 | 0.250625 | 0.375625 | s | False | |
| 3 | 0.375625 | 0.496750 | ah | False | |
| 4 | 0.496750 | 0.513000 | tcl | False | |
| ... | ... | ... | ... | ... | ... |
| mgaw0_si535 | 23 | 1.612500 | 1.652500 | k | False |
| 24 | 1.652500 | 1.741500 | axr | False | |
| 25 | 1.741500 | 1.785875 | ix | False | |
| 26 | 1.785875 | 1.857500 | ng | False | |
| 27 | 1.857500 | 2.115000 | h# | True |
12716 rows × 4 columns
2.Brain Recordings¶
Neurosurgical patients from UCSF Medical Center or Huashan Hospital participated in the recording of brain electrical signals. High-density ECoG electrode grids (manufactured by Integra or PMT) of the same specifications were placed on the lateral surface of the temporal lobe. The electrode grid consisted of a total of 128 (16x8) contact channels, with a center-to-center spacing of 4 millimeters and an exposed contact diameter of 1.17 millimeters. During the experimental tasks, neural signals were recorded from the ECoG electrode grid using a multi-channel amplifier connected optically to a digital signal processor (Tucker-Davis Technologies). Data recording was performed using TDT Synapse software. Local field potentials were amplified and sampled at each electrode contact point at a sampling frequency of 3,052 Hz. The signal was processed by noise reduction and re-averaging, and the analytic amplitude of eight Gaussian filters (centered at frequencies of 70-150 Hz) was calculated using the Hilbert transform. The high-gamma signal (HG) was defined as the average analytic amplitude of these eight frequency bands, and the signal was downsampled to 100 Hz. Processing the directly recorded signals is highly complex, and the authors provide limited data for demonstration purposes.
subject = 'HS11'
all_hgs = [preanalysis.load_hg(subject, block) for block in range(9, 11)]
all_times = [preanalysis.load_times(subject, block) for block in range(9, 11)]
all_names = [timit.get_timit_names_for_timit_block(1), timit.get_timit_names_for_timit_block(5)]
len(all_hgs),all_hgs[0].shape,all_times[0].shape,len(all_names[0])
(2, (128, 32600), (1, 124), 124)
The high-gamma signal has two blocks, and each block has an HG size of (128, 32600). Here, 128 represents the number of electrodes, and 32600 represents the number of stimulation time points. With a sampling rate of 100Hz, this means that each block corresponds to 326 seconds, approximately equivalent to 5 minutes.
3.Find Speech Responsive Channels¶
The signal is received by a 16x8 electrode grid, and not all electrodes correspond to regions relevant to speech response. We want to know which channels show significant neural signal changes to the onset of speech. Before conducting a statistical significance test for pre-post differences, we need to construct paired samples.
In many neural signal experiments, a period of time before the event of interest (in this case, the onset of speech) is included to serve as a baseline or control period. This allows for the comparison of neural activity during the event with the neural activity when the event is not happening. During a stimulus event, the HG signal from -0.2s to 1.0s (which consists of 120 neural signals) is used to create pairs of samples before and after speech onset. In total, we obtained 224 stimuli across two experimental blocks.
# get_timelocked_activity returns an array of shape (n_chans, n_timepoints, n_trials)
# which has hg activity that is timelocked to times (in seconds).
# Default time course returned is -0.2s to 1.0s.
Y_mats = []
for onsets_one_block, hg in zip(all_times, all_hgs):
Y_mats.append(erps.get_timelocked_activity(onsets_one_block, hg))
print(Y_mats[-1].shape)
Y_mats = np.concatenate(Y_mats, axis=2)
print(Y_mats.shape)
(128, 120, 124) (128, 120, 100) (128, 120, 224)
The Y_mat_before_onset averages the neural signals between 0.2s before speech onset and 0.1s after it. The Y_mat_after_onset averages the neural signals between 0.15s and 1.0s after speech onset (often referred to as the “neural latency”). These form paired samples. A paired-sample t-test (ttest_rel function) was conducted for each channel to compare the signal strength change before and after speech stimulation and determine if there was a significant difference. Then we selects the indices where the p-value is less than 0.01/len(results.pvalue). This is a way of applying a Bonferroni correction to control the family-wise error rate in the multiple comparisons of p-values.
# find speech responsive channels
Y_mat_before_onset = np.nanmean(Y_mats[:, :30, :], axis=1)
Y_mat_after_onset = np.nanmean(Y_mats[:, 35:, :], axis=1)
results = ttest_rel(Y_mat_before_onset, Y_mat_after_onset, axis=1)
responsive_chans = np.arange((len(results.pvalue)))[results.pvalue < 0.01/(len(results.pvalue))]
print("speech responsive channels: #", len(responsive_chans))
print(responsive_chans)
speech responsive channels: # 54 [ 37 38 39 40 41 48 49 50 52 53 54 55 56 57 58 64 65 66 67 68 69 70 71 72 73 74 76 80 81 82 83 84 85 86 87 88 89 90 96 97 98 99 100 101 102 103 104 112 113 114 116 118 119 121]
The channels with significant levels of p < 0.01 are printed above. In the figure below, it can be seen that the channels identified as having significant differences before and after the stimulus onset indeed exhibit larger amplitude changes.
fig, axs = plt.subplots(8, 16, figsize=(25, 15))
axs = axs.flatten()
xvals = np.linspace(-0.2, 1, 120)
for i in range(128):
plotting.plot_filled_sem(Y_mats[i], xvals, ax= axs[i], xlabel="", ylabel="",ylim=(-1,2.5), color='b')
if i in responsive_chans:
axs[i].text(0.55,0.8, '*', color='r')
for i, ax in enumerate(axs):
ax.set(yticklabels=[], xticklabels=[], xticks=[0, 1])
_ = ax.text(0.55, 0.85, str(i+1), transform=ax.transAxes)
_ = axs[-16].set(yticks=[-1, 0, 1, 2], yticklabels=[-1, 0, 1, 2], xticklabels=[0, 1], xlabel="Time (s)", ylabel="High-gamma \n(z-score across block)")
The figure below shows ECoG grid coverage. Significant speech responsive electrodes are marked in color.
fig = plt.figure(figsize=(8, 4))
gs_brains = matplotlib.gridspec.GridSpec(1, 2, width_ratios=[0.7, 1], hspace=0.1)
ax_brain = plt.subplot(gs_brains[0])
ax_inset = plt.subplot(gs_brains[1])
plotting.brain_inset([ax_brain, ax_inset], subject='HS11', response_channels=responsive_chans)
4.Time-delayed linear encoding models (TRF models)¶
The TRF model allows us to predict neural activity based on the stimulus features preceding the neural activity. Specifically, for each electrode channel, we fit a linear model given by:
$$ y(t) = \sum_{f=1}^{F} \sum_{t=1}^{T} \boldsymbol \beta_f^F(\tau) \boldsymbol x_f(t - \tau) + \epsilon $$
where $y$ is the recorded high-gamma activity on the electrode, $\boldsymbol x_f(t - \tau)$ is the stimulus representation vector of feature $f$ at time $t - \tau$, $\boldsymbol \beta_f^F(\tau)$ represents the regression weights of feature set $f$ at time lag $\tau$, and $\epsilon$ represents Gaussian noise.
To prevent overfitting, L2 regularization and cross-validation are employed in the computations. Specifically, the data is divided into three mutually exclusive sets in proportions of 80%, 10%, and 10%. The first set (80% of the samples) is used as the training set. The second set is used to optimize the hyperparameters of L2 regularization, and the last set is used as the test set. The correlation between the actual and predicted values on the held-out data is used to evaluate the model. This process is repeated five times, and the performance of the model is computed as the average performance across all test sets.
from asccd import temporal_receptive_field as trf
delays = trf.get_delays(delay_seconds=0.4)
stim_resp = trf.get_trf_stim_resp(all_hgs, all_times, all_names)
The features used here include a 30-dimensional spectral feature (although the paper describes the use of a filterbank with 161 frequency components for the FFT), a one-dimensional intensity feature, and multiple derived versions of pitch features. I annotated these features to better understand what is happening. The number 224 corresponds to the number of stimulus events, which is consistent with the previous section. For the 224 speech stimuli, the first stimulus lasted for 165 time units, which is equivalent to 16.5 seconds.
all_spec_features = stim_resp[0] # length 224, first item has shape (165, 30)
all_intensity_features = stim_resp[1] # length 224, first item has shape (165, 1)
all_binary_pitch_features = stim_resp[2] # length 224, first item has shape (165, 1)
all_abs_pitch_features = stim_resp[3] # length 224, first item has shape (165, 10)
all_rel_pitch_features = stim_resp[4] # length 224, first item has shape (165, 10)
all_pitch_change_features = stim_resp[5] # length 224, first item has shape (165, 10)
all_Y = stim_resp[6] # length 224, first item has shape (165, 128)
Fundamental frequency (F0) is a challenging feature in the real world, as it is easily affected by environmental noise. The F0 used in the experiment was calculated using the autocorrelation method in Praat, with some corrections made to rectify octave doubling and halving errors. Additionally, some derived pitch features were extracted:
- Absolute pitch is defined as the natural logarithm of the F0 value in hertz.
- Relative pitch is calculated by z-score standardizing the absolute pitch values (log(F0)) for each sentence/paragraph within a speaker.
- Pitch variation is obtained by calculating the first derivative (finite difference) of log(F0) over time.
We discretized the absolute pitch, relative pitch, and pitch variation into 10 equally spaced bins ranging from the 2.5th percentile to the 97.5th percentile values. The values below the 2.5th percentile and above the 97.5th percentile were placed in the bottom and top bins, respectively. Therefore, absolute pitch, relative pitch, and pitch variation were represented as three 10-dimensional binary feature vectors. For non-pitch periods, these feature vectors had zero values in all dimensions. The code below demonstrates the quantization process:
def get_bin_edges_percent_range(a, bins=10, percent=95):
assert percent > 1
assert percent < 100
tail_percentage = (100 - percent)/2
a = a[~np.isnan(a)]
a_range = np.percentile(a, [tail_percentage, 100-tail_percentage])
counts, bin_edges = np.histogram(a, bins=bins, range=a_range)
return bin_edges
corpus_pitch = timit.get_timit_annotations()
abs_bin_edges = get_bin_edges_percent_range(corpus_pitch['abs_pitch'])
abs_bin_edges.shape,abs_bin_edges
((11,),
array([-1.56828262, -1.21747101, -0.8666594 , -0.51584779, -0.16503618,
0.18577543, 0.53658704, 0.88739865, 1.23821026, 1.58902187,
1.93983349]))
Now, let's put these features together. The dataset used for training TRF models consists of 42,010 data samples, with each sample having 62-dimensional features (30+1+1+10+10+10). Ys represents the high gamma signals from 128 electrodes. We will use this data to train the temporal response function (TRF) models.
features_full, Ys = trf.concatenate_trf_stim_resp(stim_resp, exclude=None)
features_full.shape, Ys.shape
((42010, 62), (42010, 128))
test_corr_folds_chin, wts_folds_chin, best_alphas = trf.run_cv_temporal_ridge_regression_model(features_full, Ys, delays=delays, add_edges=False)
r2_full = np.mean(test_corr_folds_chin**2, axis=0) # r2 metric see more in paper section "Encoding models".
wts_full = np.mean(wts_folds_chin, axis=0)
Running fold 0. Running fold 1. Running fold 2. Running fold 3. Running fold 4.
wts_folds_chin.shape
(5, 2480, 128)
wts_folds_chin is the regression weight that performs best on the development set. wts_full is the average result of wts_folds_chin in the first dimension, obtained by averaging over 5 rounds of training. 2480 is the result of multiplying 40 by 62, where 40 represents 400ms and 62 is the dimension of the features. Below are the weight heatmaps for the 69th and 85th electrodes within a 400ms time window.
wts1_labels = {'yticks':(0, 3, 6, 9), 'yticklabels':(5.7, 0.2, -5.3, -10.8), 'ylabel':"Pitch change (oct/s)"}
fig = trf.plot_trf(wts_full.T, 69, wts1_label=wts1_labels, wts_shape=(40, 62), wts1=(52, 62), wts2=(42, 52), min_max=(42,62), edges_added=False, figsize=(10,3))
fig = trf.plot_trf(wts_full.T, 85, wts1_label=wts1_labels, wts_shape=(40, 62), wts1=(52, 62), wts2=(42, 52), min_max=(42,62), edges_added=False, figsize=(10,3))
5.Attention pattern analysis¶
See Section "DNN computations explain neural encoding predictions" in paper
This section investigates the computational mechanisms underlying representations in DNNs. We are curious whether specific types of attention computations in DNNs can explain the ability to predict brain responses. Here, we focus specifically on attention modeling for speech representations, which corresponds to neighboring phonemes and syllables of the target speech sound. The wav2vec2-base model is used as an example, and huggingface provides a convenient way to invoke it.
import torch
import torchaudio
from transformers import Wav2Vec2ForCTC,Wav2Vec2Processor
import os
processor = Wav2Vec2Processor.from_pretrained("facebook/wav2vec2-base")
model = Wav2Vec2ForCTC.from_pretrained("facebook/wav2vec2-base")
/ssd9/exec/penglinkai/miniconda3/envs/pytorch/lib/python3.8/site-packages/transformers/configuration_utils.py:380: UserWarning: Passing `gradient_checkpointing` to a config initialization is deprecated and will be removed in v5 Transformers. Using `model.gradient_checkpointing_enable()` instead, or if you are using the `Trainer` API, pass `gradient_checkpointing=True` in your `TrainingArguments`. warnings.warn(
Ignored unknown kwarg option normalize Ignored unknown kwarg option normalize Ignored unknown kwarg option normalize Ignored unknown kwarg option normalize
Some weights of Wav2Vec2ForCTC were not initialized from the model checkpoint at facebook/wav2vec2-base and are newly initialized: ['lm_head.weight', 'lm_head.bias'] You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.
timit_blocks = [1,2,3,4,5]
timit_names = []
for i in range(len(timit_blocks)):
timit_names.append(timit.get_timit_names_for_timit_block(timit_blocks[i]))
fig, ax = plt.subplots(1,1,figsize=(12,2))
cmaps = ['Greys','Purples', 'Blues', 'Greens', 'Oranges', 'Reds']
##### top
timit_name = timit_names[4][1]
[fs_t, sig_t] = wavfile.read(timit.get_wavpath(timit_name))
xvals_t = np.arange(len(sig_t))/fs_t
phon_times = np.asarray(timit_phonemes.loc[timit_name][timit_phonemes.loc[timit_name]['silence']==False]['start_time'])
phon_names = np.asarray(timit_phonemes.loc[timit_name][timit_phonemes.loc[timit_name]['silence']==False]['phn'])
phon_time_idx = util.time_to_index(phon_times, hz=fs_t)
syll_times = np.asarray(timit_syllables.loc[timit_name]['start_times'])
ax.plot(xvals_t, sig_t, linewidth=0.5, color=np.array([0.7,0.7,0.7]))
height = 41000
ax.text(syll_times[0], height, 'He', fontsize=10)
ax.text(syll_times[1], height, 'moistened', fontsize=10)
ax.text(syll_times[3], height, 'his', fontsize=10)
ax.text(syll_times[4], height, 'lips', fontsize=10)
ax.text(syll_times[5], height, 'uneasily.', fontsize=10)
for i in range(len(phon_times)):
if i != 13:
ax.text(phon_times[i]+0.001, 34500, phon_names[i], fontsize=9)
ax.axvline(phon_times[i], color=[0.6,0.6,0.6], ls='--')
for i in range(len(syll_times)):
ax.axvline(syll_times[i], color=[0.3,0.3,0.3], ls='-')
ax.axis("off")
xlim = (0, xvals_t[-1])
ax.set(xlim=xlim)
ax.set(ylim=[-25000,35000])
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax2 = ax.twinx()
fs = 100
df = timit_annotation.loc[timit_names[4][1]]
xvals = np.arange(len(df))/fs
ax2.plot(xvals, df['pitch'],color=np.array([0.3,0.3,0.9]),linewidth=3)
#ax2.set(xticks=[0,100,200])
#ax2.set(xticklabels=[0,1,2])
#ax.set(yticks=[180,220,260])
#ax.spines['bottom'].set_color('white')
ax2.spines['top'].set_color('white')
ax2.spines['right'].set_color('white')
ax2.axis("off")
ax.arrow((phon_times[7]+phon_times[6])*0.5, 16000, 0, -8000, head_width=0.03, head_length=4000, fc='k', ec='k')
# phoneme(0)
ax.add_patch(Rectangle((phon_times[6], 20000), phon_times[7]-phon_times[6], 4000, color=plt.get_cmap(cmaps[0])(0.7)))
# phoneme(-1)
ax.add_patch(Rectangle((phon_times[5], 20000), phon_times[6]-phon_times[5], 4000, color=plt.get_cmap(cmaps[1])(0.7)))
# phoneme(-2)
ax.add_patch(Rectangle((phon_times[4], 20000), phon_times[5]-phon_times[4], 4000, color=plt.get_cmap(cmaps[2])(0.7)))
# syllable(0)
ax.add_patch(Rectangle((syll_times[2], 27000), phon_times[6]-syll_times[2], 4000, color=plt.get_cmap(cmaps[3])(0.7)))
ax.add_patch(Rectangle((phon_times[7], 27000), syll_times[3]-phon_times[7], 4000, color=plt.get_cmap(cmaps[3])(0.7)))
# syllable(-1)
ax.add_patch(Rectangle((syll_times[1], 27000), syll_times[2]-syll_times[1], 4000, color=plt.get_cmap(cmaps[4])(0.7)))
# syllable(-2)
ax.add_patch(Rectangle((syll_times[0], 27000), syll_times[1]-syll_times[0], 4000, color=plt.get_cmap(cmaps[5])(0.7)))
fig.savefig("sample.png")
A specific sample from the TMIT dataset is used as an example, with phonemes and syllables labeled.
latent_feature_cnn = [] #[layers][block][sentence][time x feature]
latent_feature_ext = [] #[]
latent_feature_proj = []
latent_feature_encoder = []
latent_feature_en = []
latent_attention = []
for i in range(len(model.wav2vec2.feature_extractor.conv_layers)+1):
latent_feature_cnn.append([])
for i in range(len(model.wav2vec2.encoder.layers)+1):
latent_feature_encoder.append([])
for i in range(len(model.wav2vec2.encoder.layers)):
latent_attention.append([])
for i in range(len(timit_names)):
for j in range(len(latent_feature_cnn)):
latent_feature_cnn[j].append([])
for j in range(len(latent_feature_encoder)):
latent_feature_encoder[j].append([])
for j in range(len(latent_attention)):
latent_attention[j].append([])
latent_feature_ext.append([])
latent_feature_proj.append([])
latent_feature_en.append([])
for j in range(len(timit_names[i])):
sound_file = timit.get_wavpath(timit_names[i][j])
speech_array, sampling_rate = torchaudio.load(sound_file)
# feature extraction
lat = []
lat.append(speech_array.unsqueeze_(0))
for k in range(len(model.wav2vec2.feature_extractor.conv_layers)):
lat.append(model.wav2vec2.feature_extractor.conv_layers[k](lat[k]))
for k in range(len(lat)):
latent_feature_cnn[k][i].append(np.squeeze(lat[k].cpu().detach().numpy()))
lat_p, ext_feat = model.wav2vec2.feature_projection(lat[-1].permute(0,2,1))
lat_e = model.wav2vec2.encoder(lat_p, output_hidden_states=True, output_attentions=True)
# encoder layers
for k in range(len(lat_e.hidden_states)):
latent_feature_encoder[k][i].append(np.squeeze(lat_e.hidden_states[k].cpu().detach().numpy()))
for k in range(len(lat_e.attentions)):
latent_attention[k][i].append(np.squeeze(lat_e.attentions[k].cpu().detach().numpy()))
latent_feature_ext[i].append(np.squeeze(lat[-1].cpu().detach().numpy()).T)
latent_feature_proj[i].append(np.squeeze(lat_p.cpu().detach().numpy()))
latent_feature_en[i].append(np.squeeze(lat_e.last_hidden_state.cpu().detach().numpy()))
Iterate through the entire dataset and collect the representations of each sample's CNN and Transformer encoder layers at each layer.
feature_names = ['fs_ext', 'fs_proj', 'encoder0', 'encoder1', 'encoder2', 'encoder3', 'encoder4', 'encoder5',
'encoder6', 'encoder7', 'encoder8', 'encoder9', 'encoder10', 'encoder11', 'encoder12',
'hg', 'spectrogram', 'intensity', 'bin_pitch', 'abs_pitch', 'rel_pitch',
'pitch_change', 'phonetics']
nn_features = ['fs_ext', 'fs_proj', 'encoder0', 'encoder1', 'encoder2', 'encoder3', 'encoder4', 'encoder5',
'encoder6', 'encoder7', 'encoder8', 'encoder9', 'encoder10', 'encoder11', 'encoder12']
all_latent_features = {'fs_ext': latent_feature_ext,
'fs_proj': latent_feature_proj,
'encoder0': latent_feature_encoder[0],
'encoder1': latent_feature_encoder[1],
'encoder2': latent_feature_encoder[2],
'encoder3': latent_feature_encoder[3],
'encoder4': latent_feature_encoder[4],
'encoder5': latent_feature_encoder[5],
'encoder6': latent_feature_encoder[6],
'encoder7': latent_feature_encoder[7],
'encoder8': latent_feature_encoder[8],
'encoder9': latent_feature_encoder[9],
'encoder10': latent_feature_encoder[10],
'encoder11': latent_feature_encoder[11],
'encoder12': latent_feature_encoder[12]
}
stim_resp = trf.get_all_features(all_hgs, all_times, all_names, feature_names, nn_features, all_latent_features)
feat_mat = trf.concatenate_all_features(stim_resp, feature_names)
For the analysis of attention weights, a template is needed to capture patterns. Specifically,
For a given speech sentence, assuming the embedding sequence in the transformer layer as $T(c_1,...,c_T)$, where phoneme boundaries are indexed as $p_1,...,p_m$, and syllable boundaries are indexed as $s_1,...,s_n$. The attention template is defined as follows:
For the current phoneme, phoneme(0):$A_{ph(0)} \in \mathbb{R}^{T \times T}$ $$ \begin{equation} A_{ph(0)}(i,j) = \left\{ \begin{array}{**lr**} 1 & \mathrm{if\ } p_k \leq i \le p_{k+1} \mathrm{\ and \ } p_{k} \leq j \le p_{k+1} \mathrm{for\ any\ k}\\ 0 & \mathrm{otherwise} \end{array} \right. \end{equation} $$
For the previous phoneme before the current phoneme, phoneme(-1):$A_{ph(-1)} \in \mathbb{R}^{T \times T}$
$$ \begin{equation} A_{ph(-1)}(i,j) = \left\{ \begin{array}{**lr**} 1 & \mathrm{if\ } p_k \leq i \le p_{k+1} \mathrm{\ and \ } p_{k-1} \leq j \le p_{k} \mathrm{for\ any\ k}\\ 0 & \mathrm{otherwise} \end{array} \right. \end{equation} $$
For the phoneme before the previous phoneme before the current phoneme, phoneme(-2):$A_{ph(-2)} \in \mathbb{R}^{T \times T}$
$$ \begin{equation} A_{ph(-2)}(i,j) = \left\{ \begin{array}{**lr**} 1 & \mathrm{if\ } p_k \leq i \le p_{k+1} \mathrm{\ and \ } p_{k-2} \leq j \le p_{k-1} \mathrm{for\ any\ k}\\ 0 & \mathrm{otherwise} \end{array} \right. \end{equation} $$
For the current syllable, syllable(0):$A_{sy(0)} \in \mathbb{R}^{T \times T}$. Specifically, the influence of the current phoneme is excluded.$A_{sy(0)}=A_{sy(0)}-A_{ph(0)}$
$$ \begin{equation} A_{sy(0)}(i,j) = \left\{ \begin{array}{**lr**} 1 & \mathrm{if\ } s_k \leq i \le s_{k+1} \mathrm{\ and \ } s_{k} \leq j \le s_{k+1} \mathrm{for\ any\ k}\\ 0 & \mathrm{otherwise} \end{array} \right. \end{equation} $$
For the previous syllable, syllable(-1):$A_{sy(-1)} \in \mathbb{R}^{T \times T}$
$$ \begin{equation} A_{sy(-1)}(i,j) = \left\{ \begin{array}{**lr**} 1 & \mathrm{if\ } s_k \leq i \le s_{k+1} \mathrm{\ and \ } s_{k-1} \leq j \le s_{k} \mathrm{for\ any\ k}\\ 0 & \mathrm{otherwise} \end{array} \right. \end{equation} $$
For the previous previous syllable, syllable(-2):$A_{sy(0)} \in \mathbb{R}^{T \times T}$
$$ \begin{equation} A_{sy(-2)}(i,j) = \left\{ \begin{array}{**lr**} 1 & \mathrm{if\ } s_k \leq i \le s_{k+1} \mathrm{\ and \ } s_{k-2} \leq j \le s_{k-1} \mathrm{for\ any\ k}\\ 0 & \mathrm{otherwise} \end{array} \right. \end{equation} $$
For each sentence, the attention matrix $W_{xy}$ for the $x$th layer and $y$th attention head is computed. For all the templates, we calculate the correlation coefficient corr($W_{xy}$, $A_q$).
def get_phoneme_masks(timit_name, length):
phon_times = np.asarray(timit_phonemes.loc[timit_name][timit_phonemes.loc[timit_name]['silence']==False]['start_time'])
phon_time_idx = util.time_to_index(phon_times, hz=49)
phon_mask_idx = np.concatenate([[0], phon_time_idx, [length]])
phon_masks = []
phon_masks.append(np.zeros((length, length)))
for k in range(len(phon_mask_idx)-1): # phoneme 0
phon_masks[0][phon_mask_idx[k]:phon_mask_idx[k+1], phon_mask_idx[k]:phon_mask_idx[k+1]] = 1
phon_masks.append(np.zeros((length, length))) # phoneme -1
for k in range(len(phon_mask_idx)-2):
phon_masks[-1][phon_mask_idx[k+1]:phon_mask_idx[k+2], phon_mask_idx[k]:phon_mask_idx[k+1]] = 1
phon_masks.append(np.zeros((length, length))) # phoneme -2
for k in range(len(phon_mask_idx)-3):
phon_masks[-1][phon_mask_idx[k+2]:phon_mask_idx[k+3], phon_mask_idx[k]:phon_mask_idx[k+1]] = 1
return phon_masks
def get_syllable_masks(timit_name, length):
# syllable masks
syll_times = np.asarray(timit_syllables.loc[timit_name]['start_times'])
syll_time_idx = util.time_to_index(syll_times, hz=49)
syll_mask_idx = np.concatenate([[0], syll_time_idx, [length]])
syll_masks = []
syll_masks.append(np.zeros((length, length)))
for k in range(len(syll_mask_idx)-1): # syllable 0
syll_masks[0][syll_mask_idx[k]:syll_mask_idx[k+1], syll_mask_idx[k]:syll_mask_idx[k+1]] = 1
syll_masks.append(np.zeros((length, length)))
for k in range(len(syll_mask_idx)-2): # syllable -1
syll_masks[-1][syll_mask_idx[k+1]:syll_mask_idx[k+2], syll_mask_idx[k]:syll_mask_idx[k+1]] = 1
syll_masks.append(np.zeros((length, length)))
for k in range(len(syll_mask_idx)-3): # syllable -2
syll_masks[-1][syll_mask_idx[k+2]:syll_mask_idx[k+3], syll_mask_idx[k]:syll_mask_idx[k+1]] = 1
return syll_masks
def get_masks(timit_name, length):
phon_masks = get_phoneme_masks(timit_name, length)
syll_masks = get_syllable_masks(timit_name, length)
syll_masks[0] = syll_masks[0] - phon_masks[0]
all_masks = np.concatenate([phon_masks, syll_masks], axis=0)
return all_masks
length = latent_attention[0][4][1][0].shape[0]
phon_masks = get_phoneme_masks(timit_names[4][1], length)
syll_masks = get_syllable_masks(timit_names[4][1], length)
matplotlib.rcParams.update({'font.size': 16})
cmaps = ['Greys','Purples', 'Blues', 'Greens', 'Oranges', 'Reds']
all_masks = get_masks(timit_names[4][1], length)
fig, axs = plt.subplots(1,6, figsize=(25,5))
axs = axs.flatten()
for i in range(len(axs)):
axs[i].imshow(all_masks[i]*0.5, cmap=cmaps[i])
axs[i].plot([0, 1], [1, 0], transform=axs[i].transAxes, color=[0.5,0.5,0.5])
axs[i].set(xticklabels=[], yticklabels=[], xlabel='key', ylabel='query')
for im in plt.gca().get_images():
im.set_clim(0, 1)
axs[0].set(title='attention patterns\n phoneme(t-0)')
axs[1].set(title='phoneme(t-1)')
axs[2].set(title='phoneme(t-2)')
axs[3].set(title='syllable(t-0)')
axs[4].set(title='syllable(t-1)')
axs[5].set(title='syllable(t-2)')
[Text(0.5, 1.0, 'syllable(t-2)')]

Observing the comparison between these two figures, especially the parts with the same color. The upper figure presents the attention matrix patterns corresponding to different layers. It is easy to notice a general trend that deeper layers exhibit more contextual attention to linguistic structures (phonemes and syllables) from left to right. The alignment of attention with contextual structures reflects how the hierarchical structure of deep neural network models can extract speech-specific and linguistically relevant representations from natural speech.